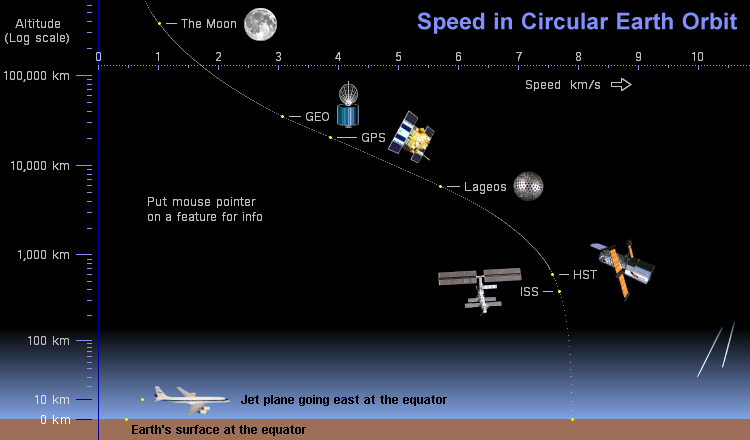
A satellite in circular orbit has a constant speed which depends only on the mass of the planet and the distance between the satellite and the center of the planet. Here are some examples of satellites in Earth orbit:

| Altitude |
r |
Speed |
Period |
Lifetime | ||||||||
| The Moon | 385,000 km | 391,370 km | 1.01 km/s | 27.3 | days | Billions of years | ||||||
| 100,000 km | 106,370 km | 1.94 km/s | 4 | days | Billions of years | |||||||
| GEO | 35,800 km | 42,170 km | 3.07 km/s | 1 | day | Millions of years | ||||||
| Navstar | 20,200 km | 26,570 km | 3.87 km/s | 12 | hours | Millions of years | ||||||
| 10,000 km | 16,370 km | 4.93 km/s | 5.8 | hours | Millions of years | |||||||
| Lageos | 5,900 km | 12,270 km | 5.70 km/s | 3.8 | hours | Millions of years | ||||||
| 2,000 km | 8,370 km | 6.90 km/s | 2.1 | hours | Millenia | |||||||
| 1,000 km | 7,370 km | 7.35 km/s | 105 | minutes | Millenia | |||||||
| Hubble | 600 km | 6,970 km | 7.56 km/s | 97 | minutes | Decades | ||||||
| ISS | 380 km | 6,750 km | 7.68 km/s | 92 | minutes | Years | ||||||
| 200 km | 6,570 km | 7.78 km/s | 89 | minutes | Days or weeks | |||||||
| 100 km | 6,470 km | 7.84 km/s | 87 | minutes | Minutes | |||||||
| Sea Level | 0 km | 6,370 km | 7.90 km/s | 84 | minutes | Seconds | ||||||
The speed (v) of a satellite in circular orbit is:
v = SQRT(G * M / r)
where G is the universal gravitational constant
Using these values gives the speed in meters per second.
The period (P) of a satellite in circular orbit is the orbit's circumference divided by the satellite's speed:
P = 2 * pi * r / v
Using values in metric units, as above, gives the period in
seconds.
Gravitational pulls from the Moon and Sun are the strongest forces
perturbing orbits of Earth satellites above
Off-center gravitational pull from Earth's equatorial bulge is
the strongest force perturbing orbits of satellites between
Atmospheric drag is the strongest force perturbing orbits of
Earth satellites below
Satellites in elliptical orbit move faster than the circular speed while near perigee, and slower than the circular speed while near apogee. The period of a satellite in any orbit, circular or elliptical, is given by Kepler's third law:
P = 2 * pi * SQRT(r3 / G * M)
where r is the mean radius of the orbit -- that is, the apogee plus the perigee (measured from the planet's center) divided by two, or half the major axis of the ellipse.
Changes to the orbit of a satellite are most efficient at
perigee and apogee. A rocket burn at perigee which increases
orbital speed raises the apogee. A burn at perigee which
decreases orbital speed lowers the apogee. Likewise, a burn
at apogee which increases orbital speed raises the perigee,
and a burn at apogee which decreases orbital speed lowers the
perigee.

Atmospheric drag on a satellite at perigee lowers the apogee,
causing the orbit to become more and more circular, until the
entire orbit is at the perigee altitude, and the satellite
soon falls from orbit.
The state of the atmosphere is also a factor. Increasing
activity in the eleven-year solar cycle heated Earth's upper
atmosphere in the late 1970s, expanding it. This increased the
drag on Skylab, which was originally at
Changes in the inclination of a satellite's orbital plane are most efficient at apogee. Large inclination changes require very large expenditures of fuel, so are rarely done. A common plane change moves geosynchronous satellites to orbit directly over the equator.
Combining a change in altitude with a change in inclination is more efficient than using a separate engine burn for each.
Whether increasing or decreasing altitude or changing orbital inclination, the most efficient engine burns are parallel to the planet's surface. When the Space Shuttle returned a large satellite to Earth, the de-orbit burn was deliberately made in an inefficient direction to use up extra fuel and lower the spacecraft's mass below the landing safety limit.
The most efficient way into orbit from Earth is to launch
directly east from the equator. This takes advantage of
Earth's rotational speed, adding it to the speed provided by
the launch vehicle. The speed at the equator is
 The S-shaped curve of orbital speeds in the graphic above is
caused by the choice of origin for the logarithmic altitude
scale. The origin is
The S-shaped curve of orbital speeds in the graphic above is
caused by the choice of origin for the logarithmic altitude
scale. The origin is
 To my Space and Science home page
To my Space and Science home page
Jeff Root
September 18, 2004